Sometimes trigonometric substitutions are very effective even when at first it may not be so clear why such a substitution be made. For example, when finding the area of a circle or an ellipse you may have to find an integral of the form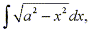 
where a>0.
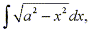where a>0.
It is difficult to make a substitution where the new variable is a function of the old one, (for example, had we made the substitution u = a2 - x2, then du= -2xdx, and we are unable to cancel out the -2x.) So we must consider a change in variables where the old variable is a function of the new one. This is where trigonometric identities are put to use. Suppose we change the variable from x to 
by making the substitution x = a sin θ. Then using the trig identity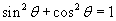 
we can simplify the integral by eliminating the root sign.
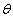by making the substitution x = a sin θ. Then using the trig identity 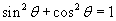we can simplify the integral by eliminating the root sign.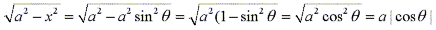
By changing x to a function with a different variable we are essentially using the The Substitution Rule in reverse. If x=g(t) then by restricting the boundaries on g we can assure that g has an inverse function; that is, g is one-to-one. In the example above we would require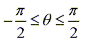 
to assure 
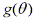has an inverse function.
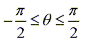to assure 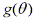has an inverse function.
If we look at the Substitution Rule and replace u with x and x with t, we obtain
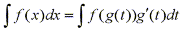
This is known as the "inverse substitution".
댓글 없음:
댓글 쓰기