Integrals of cotangent and cosecant are very similar to those with tangent and secant.
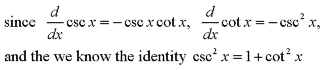
it is easy to see that integrals of the form 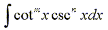 can be solved by nearly identical methods as are integrals of the form
can be solved by nearly identical methods as are integrals of the form 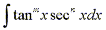 .
.
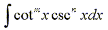 can be solved by nearly identical methods as are integrals of the form
can be solved by nearly identical methods as are integrals of the form 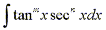 .
.
Find the indefinite trigonometric integral
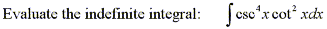 |
Solution: |
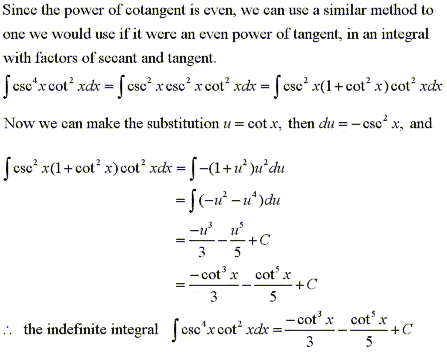 |
Unlike integrals with factors of both tangent and secant, integrals that have factors of only tangent, or only secant do not have a general strategy for solving. Use of trig identities, substitution and integration by parts are all commonly used to solve such integrals. For example,

If we make the substitution u=secx, then du=secxtanxdx, and we are left with the simple integral
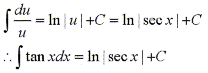
Similarily we can use the same technique to solve
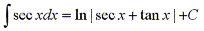
Find the definite trigonometric integral
 |
Solution: |
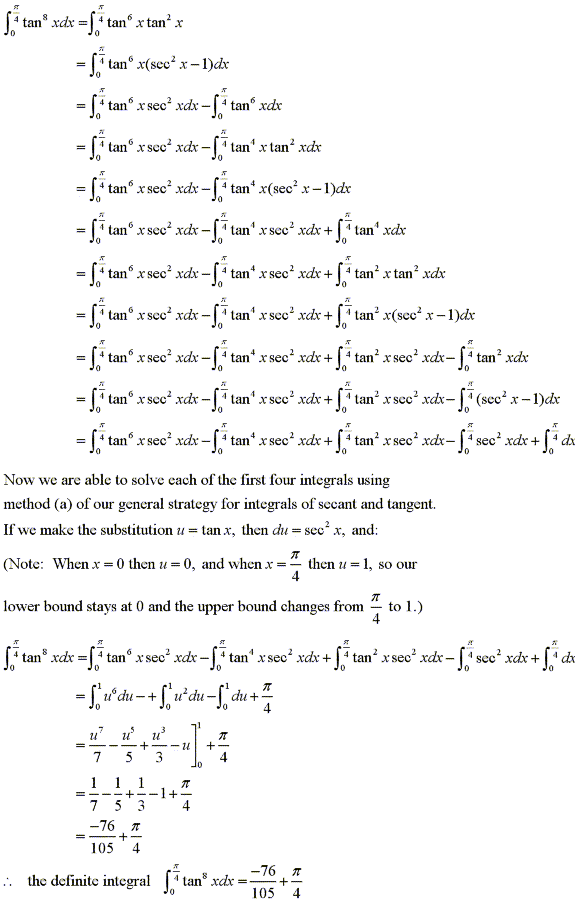 |
Find the definite trigonometric integral
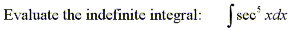 |
Solution: |
 |
Find the indefinite trigonometric integral
 |
Solution: |
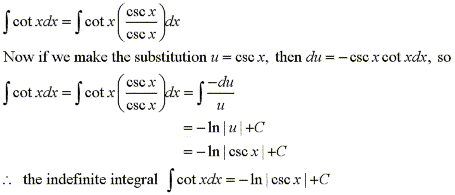 |
Another problem that may be encountered when solving trigonometric integrals are integrals of the form
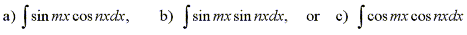
Using the product formulas which are deduced from the addition/subtraction rules we have the corresponding identities
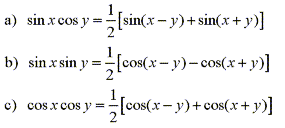
Find the indefinite trigonometric integral using the product formulas
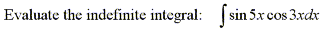 |
Solution: |
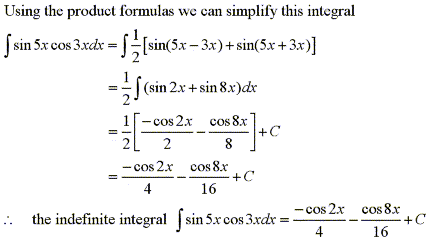 |
댓글 없음:
댓글 쓰기