Integration of Rational Functions By Partial Fractions
Integration of rational functions by partial fractions is a fairly simple integrating technique used to simplify one rational function into two or more rational functions which are more easily integrated.
Think back to the steps taken when adding or subtracting fractions that do not have the same denominator. First you find the lowest common multiple of the two denominators and then cross multiply with the numerators accordingly. eg.
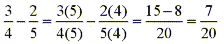
Well the same process applies when dealing with polynomial fractions. eg.
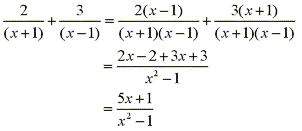
Now by reversing this process we can simplify a function such as 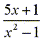 into two fractions
into two fractions 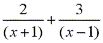 which are more easily integrated.
which are more easily integrated.
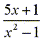 into two fractions
into two fractions 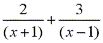 which are more easily integrated.
which are more easily integrated.
This process is possible when the function is proper; that is the degree of the numerator is less than the degree of the denominator. If the function is improper; that is the degree of the numerator is greater than or equal to the degree of the denominator, then we must first use long division to divide the denominator into the numerator until we obtain a remainder, such that it's degree is less than the denominator. Then if possible the above process is used to simplify the proper function.
To complete some of the problems in this section it will be useful to know the table integral
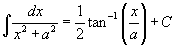
In general there are 4 cases to consider to express a rational function as the sum of two or more partial fractions.
Case 1
The denominator is a product of distinct linear factors (no factor is repeated or a constant mulptiple of another).
The denominator is a product of distinct linear factors (no factor is repeated or a constant mulptiple of another).
For example, 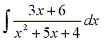
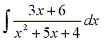
Since the degree of the numerator is less than the degree of the denominator we don't need to divide. The denominator can be factored as follows:
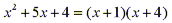
Since the denominator has distinct linear factors we can write the rational fraction as the sum of two or more partial fractions as follows:
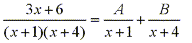
By multiplying both sides by 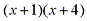 we have:
we have:
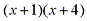 we have:
we have: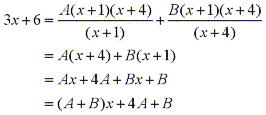
From this equation we can match terms of the same degree to determine the coefficients by solving the following system of equations:
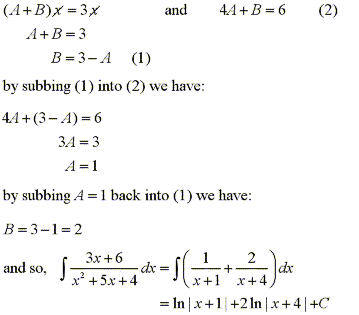
Case 2
The denominator is a product of linear functions, some of which are repeated.
For example, 

Since the degree of the numerator is greater than the degree of the denominator we must factorize by long division.
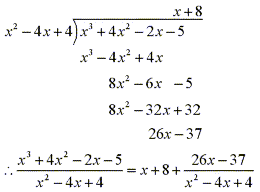
So we can now factor the denominator to obtain:
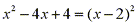
Since the linear factor (x-2) occurs twice, the partial fraction decomposition is:
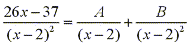
When we multiply both sides by the least common denominator we get:
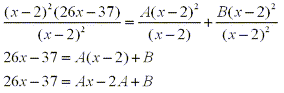
From this equation we can match terms of the same degree to determine the coefficients by solving the following system of equations:
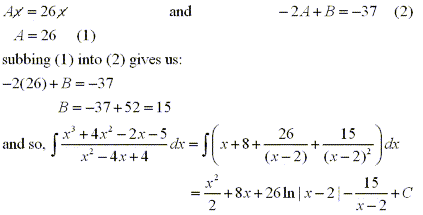
Case 3
The denominator contains irreducible quadratic factors, none of which are repeated.
When reducing such functions to partial fractions if there is a term in the denominator of the form ax2 + bx + c, where b2 - 4ac < 0, then the numerator for that partial fraction will be of the form Ax + B.
For example, 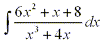
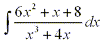
Since the degree of the numerator is less than the degree of the denominator we do not have to divide first.
Since x3 + 4x = x(x2 + 4) can't be factored any further we have:
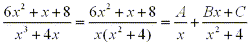
multiplying both sides by x(x2 + 4), we have:
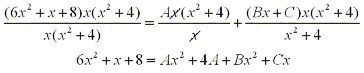
From this equation we can match terms of the same degree to determine the coefficients by solving the following system of equations:

Case 4
The denominator contains a repeated irreducible quadtratic factor.
Functions of this form are the same as those in case 3 only there is a term in the denominator that is repeated or is a constant multiple of another.
For example, 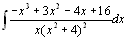
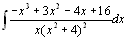
If we were to expand the denominator we would see that its degree is greater than the the degree of the numerator so we do not have to divide first.
Since the function cannot be factored any further we have:
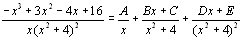
multiplying both sides by (x + 1)(x2 + 4)2, we have:
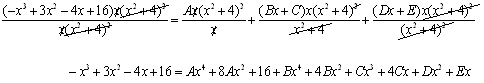
From this equation we can match terms of the same degree to determine the coefficients by solving the following system of equations:
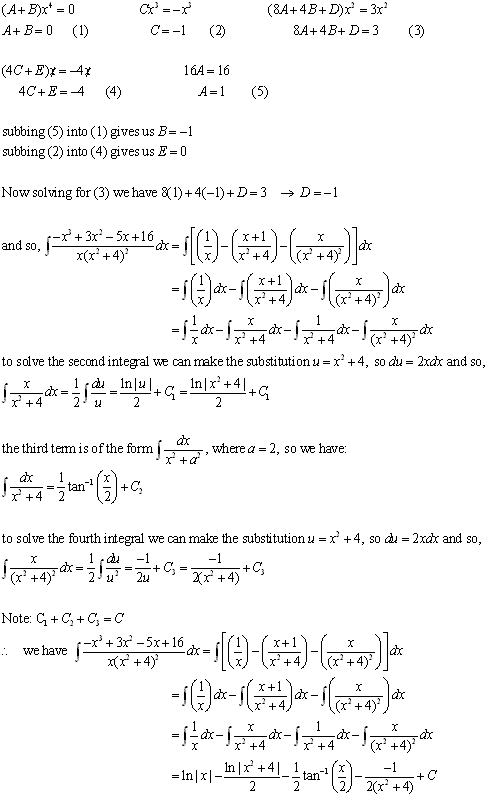
Improper Integrals
In all of the previous tutorials we have dealt with integrals with a continous function f on a finite interval [a,b]. In this section we will consider two types of integrals known as improper integrals. The first type of improper integral are those defined on an infinite interval, and the second are those where the function f has an infinite discontinuity in [a,b].
Type 1: Infinite Intervals
Type 2: Discontinous Integrands
댓글 없음:
댓글 쓰기