Suppose we have an integral such as
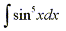
The easy mistake is to simply make the substitution u=sinx, but then du=cosxdx. So in order to integrate powers of sine we need an extra cosx factor. Similarily, in order to integrate powers of cosine we need an extra sinx factor. Thus for this example knowing we need an extra sinx factor to integrate powers of cosine we can separate one sine factor and convert the remaining sin4x to an expression involving cosine using the identity sin2x + cos2x = 1.
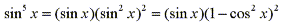
Now by using our knowledge of substitution we can evaluate the integral by letting u=cosx, then du=-sinxdx and
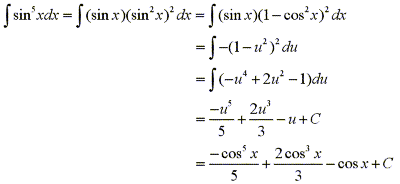
Now consider the integral
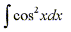
If we were to use the method from the previous example and separate one cosine factor we would be left with a factor of cosine of odd degree which isn't easily converted to sine. We must now consider the half angle formulas
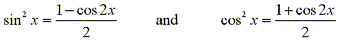
Using the half angle formula for cos2x, we have:
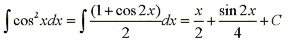
Strategy for Evaluating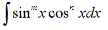
- (a)
- If the power of sine is odd (m=2k+1), save one sine factor and use the identity sin2x + cos2x = 1 to convert the remaining factors in terms of cosine.
then substitute u=cosx.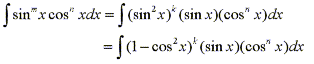
- (b)
- If the power of cosine is odd (n=2k+1), save one cosine factor and use the identity sin2x + cos2x = 1 to convert the remaining factors in terms of sine.
then substitute u=sinx.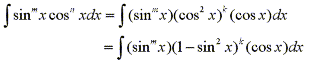
- (c)
- If the powers of both sine and cosine are even then use the half angle identities.
In some cases it may be helpful to use the identity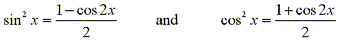
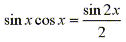
Find the indefinite trigonometric integral
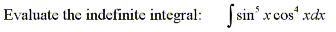 |
Solution: |
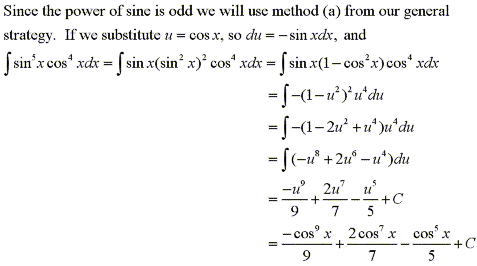 |
Using the half angle formulas solve the indefinite trigonometric integral
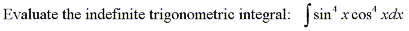 |
Solution: |
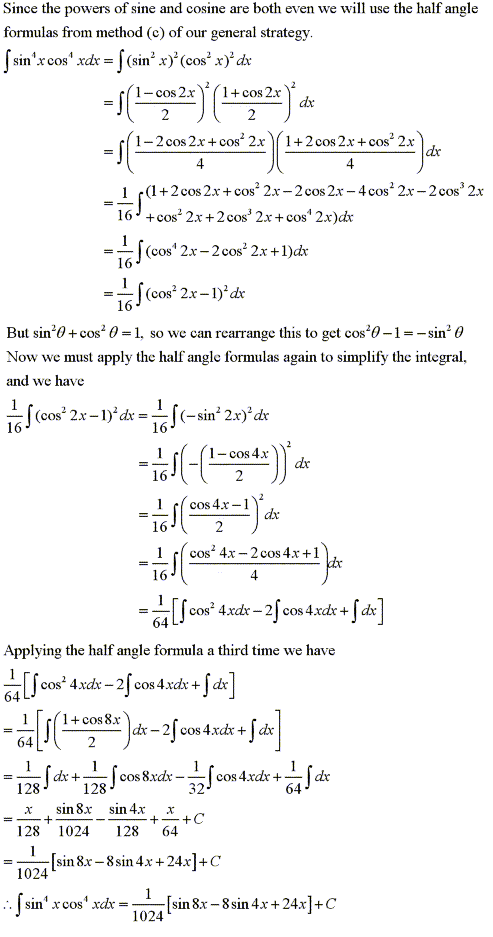 |
Find the definite trigonometric integral
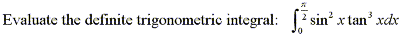 |
Solution: |
 |
댓글 없음:
댓글 쓰기