Suppose that we have an integral such as
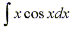
Similar to integrals solved using the substitution method, there are no general equations for this indefinite integral. However there do not appear to be any clear substitutions that could be made to simplify this integral. This brings us to an integration technique known as integration by parts, which will call upon our knowledge of the Product Rule for differentiation.
The Product Rule states: If f and g are differentiable functions, then
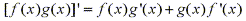
By taking the indefinite integral of both sides of the equation we have:
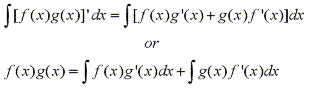
and we can rearrange this equation as
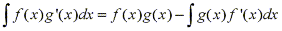
To make it easier to remember it is commonly written in the following notation. Let u=f(x) and v=g(x). Then the differentiables are du=f'(x)dx and dv=g'(x)dx, so by the substitution rule, the formula for integration by parts becomes:
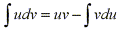
From our previous example, if we let u=x and dv=cosx, then du=dx and v=sinx. If we substitute these values into the formula we have:
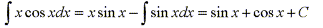
Note: By choosing u=x we obtain a simpler integral than we started with. Had we chose u=cosx and dv=x then du=-sinx and v=(1/2)x2 so integration by parts gives:
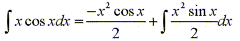
This equation is correct, but the integral is more difficult than the one we started with.
When choosing u and dv always try to choose u=f(x) to be a function that becomes simpler when differentiated (or at least not more complicated) and to choose dv=g'(x) to be a function that can be easily integrated to give v.
Examples
Find the general indefinite integral by integration by parts
 |
Solution: |
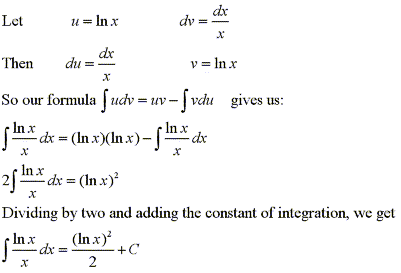 |
Evaluate the definite integral by integration by parts
 |
Solution: |
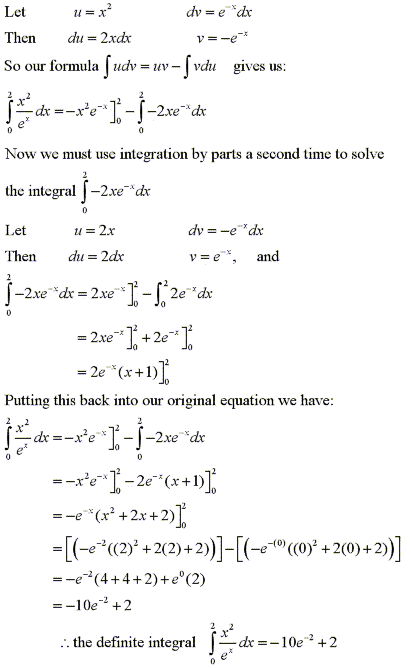 |
댓글 없음:
댓글 쓰기