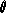
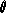
can be interpreted as the measure of the angle constructed as follows: wrap a piece of string of length units around the unit circle 
(counterclockwise if 
, clockwise if 
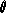
) with initial point P(1,0) and terminal point Q(x,y). This gives rise to the central angle with vertex O(0,0) and sides through the points P and Q. All six trigonometric functions of are defined in terms of the coordinates of the point Q(x,y), as follows:
Since Q(x,y) is a point on the unit circle, we know that
. This fact and the definitions of the trigonometric functions give rise to the following fundamental identities:
This modern notation for trigonometric functions is due to L. Euler (1748).
More generally, if Q(x,y) is the point where the circle
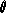
of radius R is intersected by the angle , then it follows (from similar triangles) that
Periodic Functions
If an angle
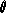
corresponds to a point Q(x,y) on the unit circle, it is not hard to see that the angle 
corresponds to the same point Q(x,y), and hence that
Moreover,
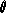
is the smallest positive angle for which Equations 1 are true for any angle . In general, we have for all angles :
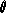
We call the number
the period of the trigonometric functions 
and 
, and refer to these functions as being periodic. Both 
and 
are periodic functions as well, with period , while 
and 
are periodic with period 
.EXAMPLE 1 Find the period of the function
.Solution: The function
runs through a full cycle when the angle 3x runs from 0 to , or equivalently when x goes from 0 to 
. The period of f(x) is then .EXERCISE 1 Find the period of the function
.Solution
Evaluation of Trigonometric functions
Consider the triangle with sides of length
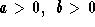
and hypotenuse c>0 as in Figure 1 below: |
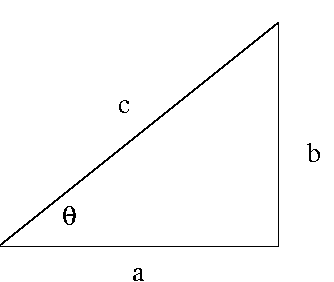| Figure 1 |
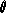
pictured in the figure, we see that |  |
 |  |
 |  |
There are a few angles for which all trigonometric functions may be found using the triangles shown in the following Figure 2.
 |
 |
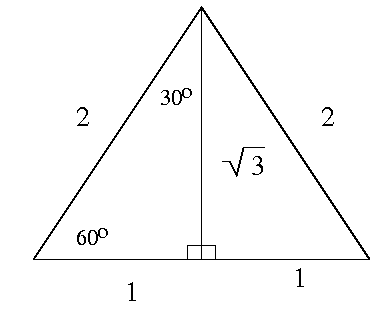| Figure 2 |
EXAMPLE 1: Find the values of all trigonometric functions of the angle
.Solution: From Figure 2, we see that the angle of
corresponds to the point 
on the unit circle, and so
EXAMPLE 2: Find the values of all trigonometric functions of the angle
.Solution: Observe that an angle of
is equivalent to 8 whole revolutions (a total of 
) plus 
, Hence the angles and intersect the unit circle at the same point Q(x,y), and so their trigonometric functions are the same. Furthermore, the angle of makes an angle of with respect to the x-axis (in the second quadrant). From this we can see that 
and hence that
We call the auxiliary angle of
the reference angle of .EXAMPLE 3 Find all trigonometric functions of an angle
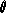
in the third quadrant for which 
.Solution: We first construct a point R(x,y) on the terminal side of the angle
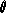
, in the third quadrant. If R(x,y) is such a point, then 
and we see that we may take x=-5 and R=6. Since 
we find that 
(the negative signs on x and y are taken so that R(x,y) is a point on the third quadrant, see Figure 3). |
| Figure 3 |
S.O.S.mathmatics
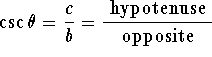
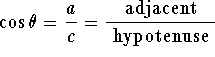
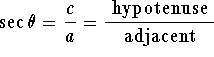
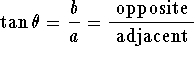
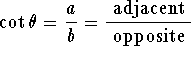
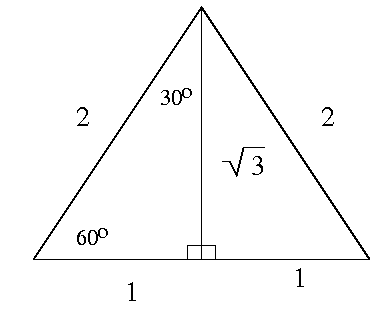
댓글 없음:
댓글 쓰기