2) The magic identity

Trigonometry is the art of doing algebra over the circle. So it is a mixture of algebra and geometry. The sine and cosine functions are just the coordinates of a point on the unit circle. This implies the most fundamental formula in trigonometry (which we will call here the magic identity)

where  is any real number (of course  measures an angle).
Example. Show that


Answer. By definitions of the trigonometric functions we have

Hence we have

Using the magic identity we get

This completes our proof.
Remark. the above formula is fundamental in many ways. For example, it is very useful in techniques of integration.
Example. Simplify the expression


Answer. We have by definition of the trigonometric functions

Hence

Using the magic identity we get

Putting stuff together we get

This gives

Using the magic identity we get

Therefore we have





Example. Check that


Answer. Use the definitions of the trigonometric functions to get

Hence we have

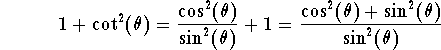
Using the magic identity we get

This completes our proof.



Example. Simplify the expression


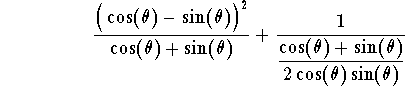
answer. Using algebra, we have

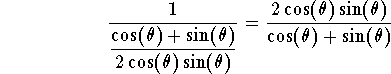
Hence

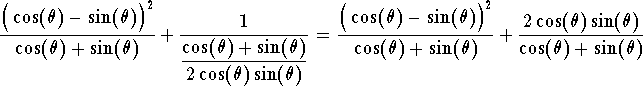
which gives

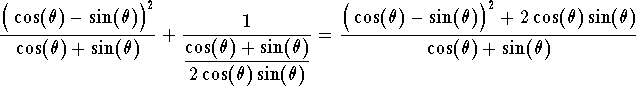
Since  , we get




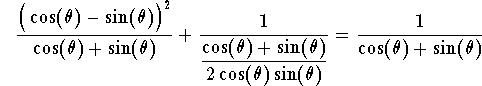
The following identities are very basic to the analysis of trigonometric expressions and functions. These are called Fundamental Identities

Reciprocal identities





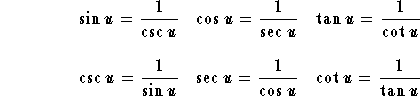
Pythagorean Identities



Quotient Identities



S.O.S.mathmatics