Volumes
Integration also allows us to calculate the volumes of solids. Let S be a solid that lies between x=a and x=b. Let the continuous function A(x) represent the cross-sectional area of S in the plane through the point x and perpendicular to the x-axis. The volume of S is given by
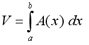
Now that we have the definition of volume, the challenging part is to find the function of the area of a given cross section. This process is quite similar to finding the area between curves.
Most volume problems that we will encounter will be require us to calculate the volume of a solid of rotation. These are solids that are obtained when a region is rotated about some line. A typical volume problem would ask, "Find the volume of the solid obtained by rotating the region bounded by the curve(s) about some specified line." Since the region is rotated about a specific line, the solid obtained by this rotation will have a disk-shaped cross-section. We know from simple geometry that the area of a circle is given by A = p r2. For each cross-sectional disk, the radius is determined by the curves that bound the region. If we sketch the region bounded by the given curves, we can easily find a function to determine the radius of the cross-sectional disk at point x.
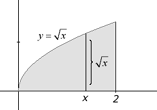 | 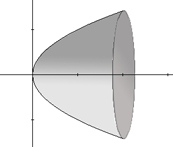 |  |
The figures above illustrates this concept. The figure to the left shows the region bounded by the curve 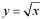 and the x-axis and the lines x = 0 and x = 2. The figure in the center shows the 3-dimensional solid that is formed when the region from the first figure is rotated about the x-axis. The figute to the right shows a typical cross-sectional disk. A disk for a given value x between 0 and 2 will have a radius of
and the x-axis and the lines x = 0 and x = 2. The figure in the center shows the 3-dimensional solid that is formed when the region from the first figure is rotated about the x-axis. The figute to the right shows a typical cross-sectional disk. A disk for a given value x between 0 and 2 will have a radius of 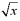 . The area of the disk is given by A(x) = p (
. The area of the disk is given by A(x) = p (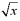 )2 or equivalently, A(x) = px. Once we find the area function, we simply integrate from a to b to find the volume. The examples below will show complete solutions to finding the area of a given solid.
)2 or equivalently, A(x) = px. Once we find the area function, we simply integrate from a to b to find the volume. The examples below will show complete solutions to finding the area of a given solid.
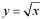 and the x-axis and the lines x = 0 and x = 2. The figure in the center shows the 3-dimensional solid that is formed when the region from the first figure is rotated about the x-axis. The figute to the right shows a typical cross-sectional disk. A disk for a given value x between 0 and 2 will have a radius of
and the x-axis and the lines x = 0 and x = 2. The figure in the center shows the 3-dimensional solid that is formed when the region from the first figure is rotated about the x-axis. The figute to the right shows a typical cross-sectional disk. A disk for a given value x between 0 and 2 will have a radius of 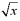 . The area of the disk is given by A(x) = p (
. The area of the disk is given by A(x) = p (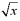 )2 or equivalently, A(x) = px. Once we find the area function, we simply integrate from a to b to find the volume. The examples below will show complete solutions to finding the area of a given solid.
)2 or equivalently, A(x) = px. Once we find the area function, we simply integrate from a to b to find the volume. The examples below will show complete solutions to finding the area of a given solid.Variations of Volume Problems
There are several variations in these types of problems. The first factor that can vary in a volume problem is the axis of rotation. What if the region from the figure above was rotated about the y-axis rather than the x-axis? We would end up with a different function for the radius of a cross-sectional disk. The function would be written with respect to y rather than x, so we would have to integrate with respect to y. In general, we can use the following rule.
If the region bounded by the curves f(x) and g(x) and the lines x=a and x=b is rotated about an axis parallel to the x-axis, write the integral with respect to x. If the axis of rotation is parallel to the y-axis, write the integral with respect to y.
The second factor that can vary in volume problems is the radius of a typical cross-sectional disk. Suppose that the region is bounded by two curves, f(x) and g(x), that both vary between x=a and x=b. The solid that is created by rotating this region about some specified line will have a hole in the center. The radius of a cross-sectional disk will be determined by two functions, rather than a single function. This variation creates two separate styles of problems.

The Disk Method : The disk method is used when the cross sections are disk shaped. The radius of a cross section is determined by a single function, f(x). The area of the disk is given by the formula, A(x) = p (radius)2. The figure to the right shows a typical cross-sectional disk.
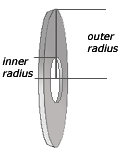
The Washer Method : The washer method is used when the cross sections are washer shaped. The radius of a cross section is determined by a two functions, f(x) and g(x). This gives us two separate radii, an outer radius, from f(x) to the axis of rotation and an inner radius from g(x) to the axis of rotation. The area of the washer is given by the formula, A(x) = p [ (outer radius)2-(inner radius)2 ]. The figure to the left shows a typical cross-sectional washer.
댓글 없음:
댓글 쓰기