Volumes By Cylindrical Shells

There is another method to solve volume problems, in addition to the methods described in the section above. The method of cylindrical shells is sometimes simpler to use than the previous methods. For example, suppose we want to find the volume of the solid obtained by rotating about the y-axis, the region bounded by the y=3x-x³ and the line y=0. Since the axis of rotation is parallel to the y-axis, we must integrate the area function with respect to y. To do this, We must solve the cubic function for x in terms of y. This would be rather difficult. However, we will soon see that this problem can be solved quite easily using the method of cylindrical shells.

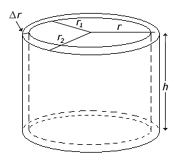
The image to the right shows a cylindrical shell with outer radius r₂, inner radius r₁ and height h. We can calculate the volume of the shell by finding the volume of the inner cylinder, V₁ and subtracting it from the volume of the outer cylinder, V₂. Recall from the geometry tutorial, that the volume of a cylinder is given by the formula V = pi r²h.

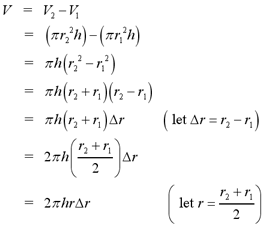
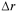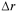We let  represent the thickness of the cylindrical shell and r represent the average radius of the shell. In summary, the volume of a cylindrical shell is given by the following formula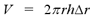

Now that we have covered the concept of a cylindrical shell, we can apply it to general volume problems. The idea behind the method of cylindrical shells is to think of a 3-dimensional solid as a collection of cylindrical shells. To find the volume of the solid, we must integrate the formula for the volume of a cylindrical shell. However, the formula for the volume of the cylindrical shell will vary with each problem. We must find functions for the height and the radius of the cylindrical shell at x. Suppose the functions are h(x) for height and r(x) for radius. The volume of the solid obtained by rotating a region about a specific line from a to b is given by

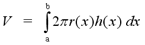
This may seem complicated, but after a few examples the method will be much clearer.

Nipissing University