Areas Between Curves

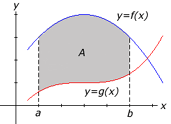
The area A of the region bounded by the curves, f(x) and g(x), and the lines x=a and x=b, where f and g are continuous and f(x)>g(x) for all x in the interval [a, b], is given by

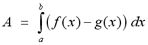
The figure to the right illustrates the region that is given by the definition above. To make the image clearer, the curve f(x) is shown in blue and the curve g(x) is shown in red.

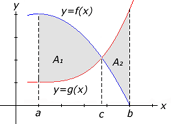
In some problems, the curves may intersect so that f(x) is not greater than g(x) over the entire interval [a, b]. The graph to the right illustrates this situation. In this case, we must find the point of intersection, c, between the two curves. To find the point of intersection c, we set f(x) = g(x) and solve the resulting equation for x. To find the area, we split the region A between the curves into 2 separate regions, A₁, bounded by f(x) and g(x) and the lines x=a and x=c, and A₂, bounded by g(x) and f(x) and the lines x=c and x=b. To find the area of A, we calculate the area of each individual region and take the sum of the results.

For the curve to the right, the equation for the area of the region would be given by

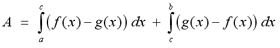
Note: This equation depends on the nature of the question. Not all problems will use this same equation to determine the area. For example, if the curve g(x) is greater than f(x) on [a,c), and less than f(x) on (c,b], we would switch the f(x) with g(x) in the equation above.

In other problems, the region may be bounded by the curves f(x) and g(x) over part of the interval [a,b] but may be bounded by only a single curve for another part of the interval. The figure below illustrates this situation.

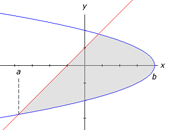
In a problem like this, there are two possible solutions.

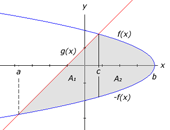
a) The first method is to find the point of intersection, c, between the two curves. We split the region A between the curves into 2 separate regions, A₁, bounded by f(x) and g(x) and the lines x=a and x=c, and A₂, bounded by +f(x) and -f(x) and the lines x=c and x=b. The image to the right illustrates the first method of solving this type of area problem. The formula to the below shows how the area would be calculated for this specific example.

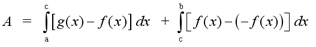
Note: Like the problem above, this equation depends on the nature of the question. You must recognize which function defines the upper boundary and which defines the lowers boundary over a certain interval.

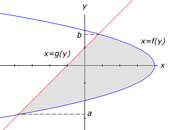
b) The second method involves rewriting the problem so that it is in terms of y rather than x. We express each curve in terms of y, so that we have f(y) for the right boundary and g(y) for the left boundary. We must find the y coordinates of the intersection points of the curves. We let y=b represent the higher intersection point and y=a represent the lower intersection point. The image to the right illustrates the second approach to solving the example above. The equation below shows how the area would be calculated for this specific example.

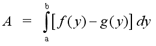
Note: Once again, this equation depends on the nature of the question.

In fact, this method can be used to solve any area problems. It may often be simpler to solve the integrals when the functions in terms of y rather than x. If the problem seems too difficult, we can always try to solve it in terms of y.

Nipissing University